パスカルの法則とは何か、またそれが油圧プレスとどのように関係しているか？実験室での力増幅を解き放つ

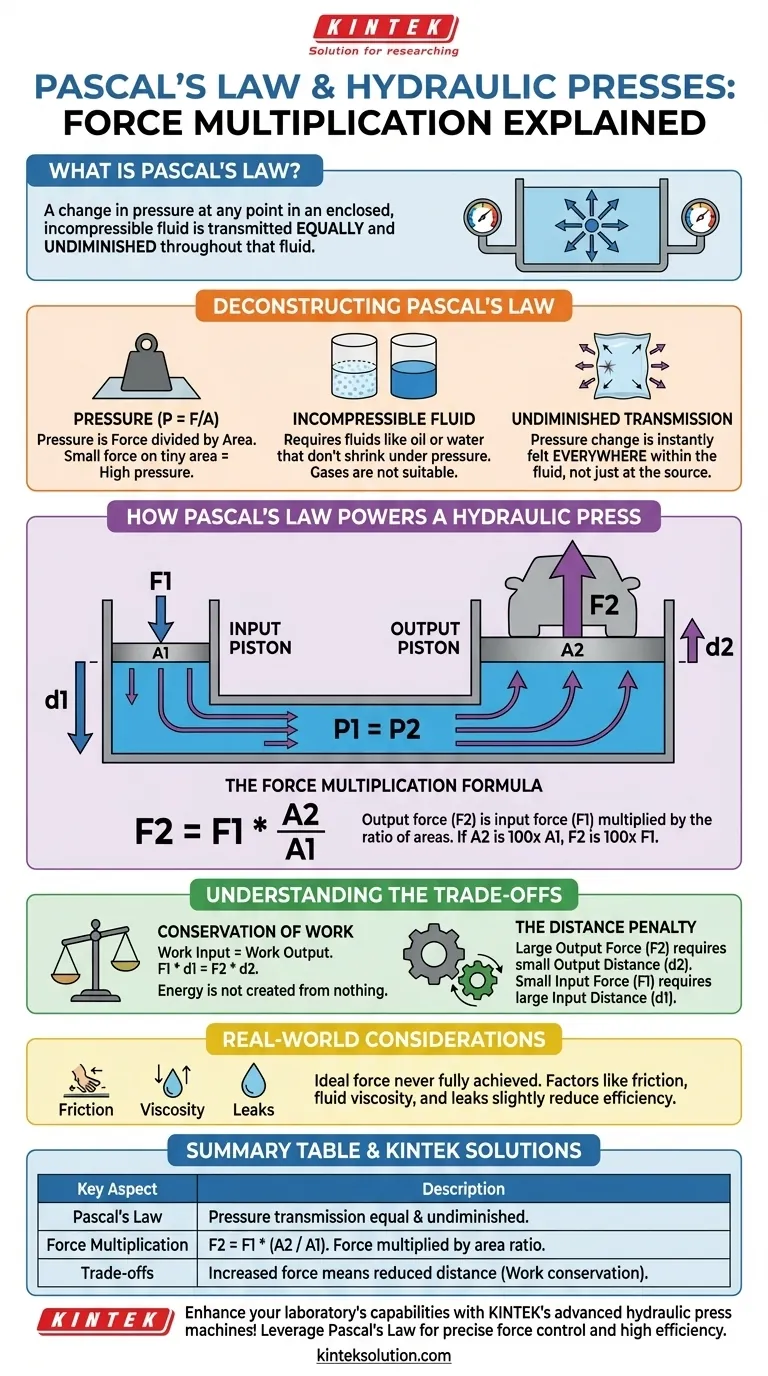
その核心において、パスカルの法則は、密閉された非圧縮性流体の任意の点における圧力の変化が、その流体全体に均等に、かつ減衰することなく伝達されると述べています。この原理は油圧プレスの基本的な仕組みであり、小さく扱いやすい力を極めて強力な力に変換することを可能にします。これは、その初期圧力をはるかに大きな面積に伝達することによって機能し、それによって生じる力を増幅させます。

パスカルの法則の中心的な洞察は、空から力を生み出しているわけではないということです。代わりに、非圧縮性流体を使用して圧力を均一に伝達し、小さな面積に加わる小さな力が、より大きな面積に作用する等しい圧力をもたらし、より大きな合計力を生み出すということです。

パスカルの法則の分解

油圧システムがどのように機能するかを真に理解するためには、まず原理自体の3つの核となる構成要素を理解する必要があります。

圧力の定義

圧力（P）は、特定の面積（A）に加えられる力（F）として定義されます。この関係は、基本式P = F/Aで表されます。

小さな力であっても、狭い面積に集中させれば、広大な面積に広がった巨大な力と同じ圧力を発生させることができます。この概念が力増幅を理解するための鍵となります。

非圧縮性流体

パスカルの法則には、油や水などの非圧縮性流体が必要です。これは、圧力が加えられたときに流体の体積が目立って減少することを意味します。

気体は圧縮性があるため、圧力を効率的に伝達する代わりに単に圧縮されてしまうため、この用途には適していません。

減衰しない伝達

これは法則の最も重要な側面です。密閉された流体の任意の部分に圧力を加えると、その全く同じ圧力が流体内のどこにでも瞬時に伝わります。

水で満たされた密閉されたビニール袋を想像してください。片側を指で突くと、指が当たっている場所だけでなく、袋全体が張り詰め、圧力が均等に上昇します。

パスカルの法則はいかにして油圧プレスを駆動するか

油圧プレスはこの原理の古典的かつ実用的な応用例です。これは、著しい力増幅を達成するために、単純な二重ピストンシステムを使用します。

二重ピストンシステム

基本的な油圧システムは、非圧縮性流体で満たされたパイプで接続された2つの円筒形ピストンで構成されています。

ピストン1（入力）: 表面積（A1）が小さい。
ピストン2（出力）: 表面積（A2）がはるかに大きい。

小さな入力（入力）力（F1）がピストン1に加えられ、流体中に圧力を発生させます。

等しい圧力、不均等な力

パスカルの法則によれば、入力ピストン（P1 = F1 / A1）によって生成された圧力は、流体全体に減衰することなく伝達されます。これは、出力ピストン（P2）に作用する圧力が全く同じであることを意味します。

したがって、P1 = P2となります。

P = F/Aであるため、代入して次の式を得ることができます：F1 / A1 = F2 / A2。

力増幅の公式

この式を並べ替えることで、出力力（F2）について解くことができます：

F2 = F1 * (A2 / A1)

これは増幅効果を優雅に示しています。出力力は、入力力を2つのピストンの面積比で乗じたものです。出力ピストンの面積が入力ピストンの面積の100倍大きい場合、力は100倍増幅されます。

トレードオフの理解

この原理は、何もないところからエネルギーを生み出すわけではありません。増幅された力には代償が伴い、これはエネルギー保存の法則によって支配されています。

仕事の保存

物理学において、仕事 = 力 x 距離です。油圧システムが平衡状態にあるためには、入力ピストンに加えられる仕事が出力ピストンによって行われる仕事と等しくなければなりません。

Work_input = Work_output F1 * d1 = F2 * d2

距離のペナルティ

出力力（F2）が入力力（F1）よりもはるかに大きいため、出力ピストンが移動する距離（d2）は、入力ピストンが移動する距離（d1）よりも比例的に小さくなければなりません。

重い車を大きなピストンで1インチ持ち上げるために、小さなピストンを数フィート押す必要があるかもしれません。力増幅のために移動距離を犠牲にするのです。

実世界の非効率性

実際のあらゆる応用において、理想的な出力力が完全に得られることはありません。ピストンとシリンダー壁間の摩擦、流体粘度、システム内の潜在的な漏れなどの要因が、すべて力の伝達の効率をわずかに低下させます。

目標に応じた適切な選択

この原理を理解することで、主な目的に基づいてターゲットを絞った設計上の決定を下すことができます。

最大の力増幅が主な焦点である場合: 出力面積（A2）と入力面積（A1）の比率を最大化する必要があります。
動作速度が主な焦点である場合: より大きな出力距離（d2）にはより小さな面積比（A2/A1）が必要となるため、より低い力増幅比を受け入れる必要があります。
実世界のシステムを設計している場合: 摩擦やその他の損失による実際の出力力は理論的な計算よりもわずかに低くなるため、必ず非効率性のための余裕を見込んでください。

最終的に、パスカルの法則は、現代の機械および産業工学の礎であり続ける、強力で洗練されたフレームワークを提供します。

要約表:

主要な側面	説明
パスカルの法則	非圧縮性流体中の圧力変化は、流体全体に均等に、減衰することなく伝達される。
力増幅の公式	F2 = F1 * (A2 / A1)。ここでF2は出力力、F1は入力力、A2は出力面積、A1は入力面積。
トレードオフ	力の増加は移動距離の減少を伴い、エネルギー保存（F1 * d1 = F2 * d2）によって支配される。
応用例	材料試験および加工における正確な力制御と高出力を提供するため、実験室での油圧プレスに最適。

KINTEKの先進的な油圧プレス機で実験室の能力を向上させましょう！ 自動ラボプレス、静水圧プレス、加熱ラボプレスのいずれが必要であっても、当社の装置はパスカルの法則を活用して、実験室のあらゆるニーズに対応する正確な力制御、高効率、信頼性の高いパフォーマンスを提供します。非効率性に足を引っ張られないようにしてください。当社のソリューションが生産性を高め、材料試験および加工において優れた結果を達成する方法については、今すぐお問い合わせください！