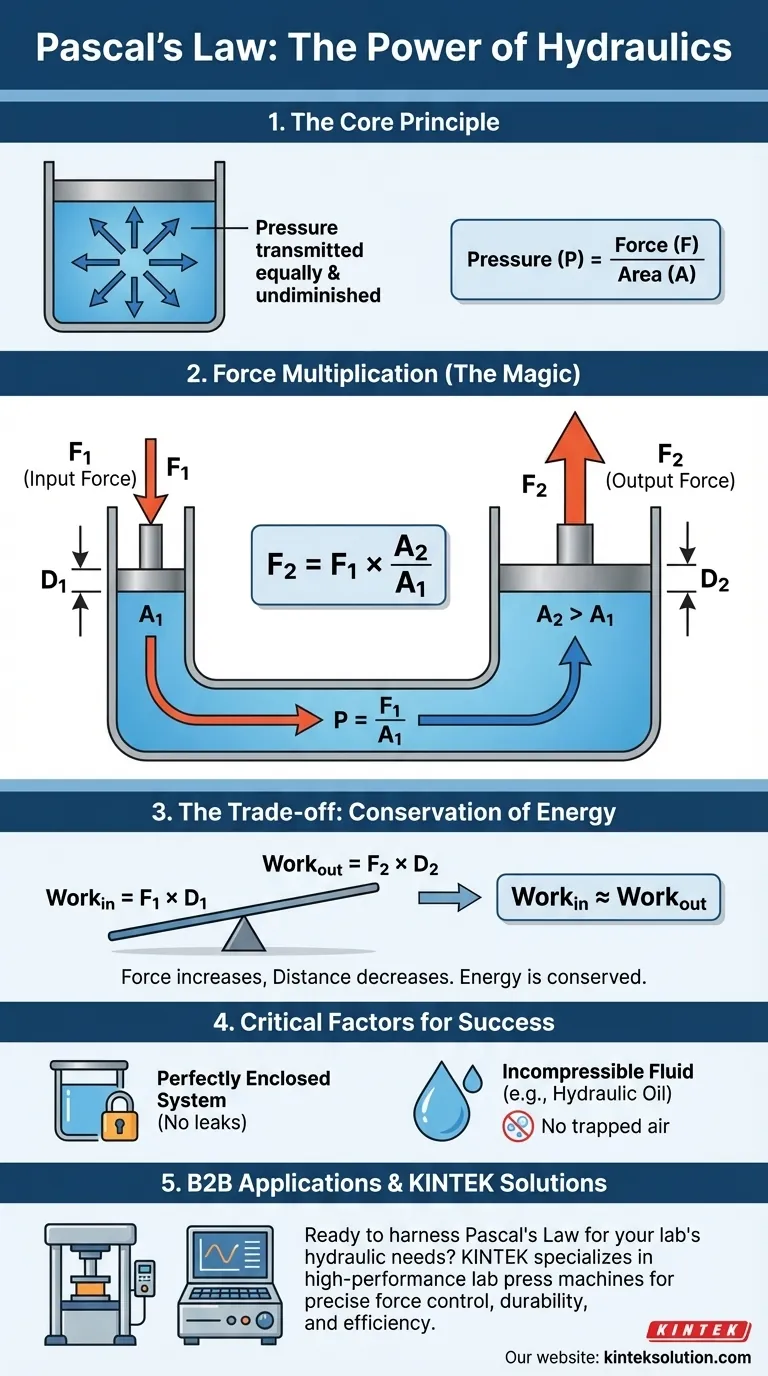
本質的に、パスカルの法則とは、密閉された非圧縮性流体の任意の点での圧力の変化が、その流体のすべての部分に均等に、減衰することなく伝達されることを述べています。これは、密閉容器内の流体に圧力を加えると、容器内のすべての場所で、まったく同じ量だけ、まったく同時に圧力が上昇することを意味します。
定義は圧力の伝達に焦点を当てていますが、パスカルの法則の真の力は、それがいかにして大規模な力倍増を達成できるかという点にあります。この単一の原理は、現代のほぼすべての油圧システムの基礎となっています。
基本方程式：圧力、力、面積
パスカルの法則の意味を理解するには、まずその3つの中心的な構成要素の関係を理解する必要があります。
圧力の定義
圧力（P）は、特定の面積（A）に加えられる力（F）として定義されます。その式は P = F/A です。
手のひら全体で押す場合と、指先一つで押す場合の違いを考えてみてください。力は同じかもしれませんが、指先の圧力は面積がはるかに小さいため、はるかに大きくなります。
非圧縮性流体の役割
パスカルの法則は、水や作動油などの非圧縮性流体の使用に依存しています。このタイプの流体に力を加えた場合、体積が小さくなるまで押しつぶされることはありません。
流体が圧縮されないため、導入されたエネルギーは他の場所に伝達されなければなりません。これが、圧力がシステム全体に瞬時に伝播する仕組みです。
力の倍増の魔法
パスカルの法則を適用する真の巧妙さは、単に圧力が伝達されることではなく、それが力の倍増に利用できるという点にあります。これは、車のジャッキから航空機の着陸装置に至るまですべての動作原理の基盤となっています。
基本的な油圧モデル
オイルで満たされ、両端がピストンで密閉されたU字管を想像してください。一方のピストンは小さく（入力ピストン）、もう一方は大きい（出力ピストン）とします。
入力力の適用
面積A1を持つ小さなピストンに小さな下向きの力（F1）を加えるとします。これにより、流体内に圧力が発生します：P = F1 / A1。
圧力の伝達
パスカルの法則によれば、この正確な圧力（P）は、流体の隅々に存在します。これには、大きな出力ピストンの真下の領域も含まれます。
出力力の計算
この同じ圧力（P）が、面積A2を持つ大きなピストンを上向きに押し上げます。結果として生じる上向きの力（F2）は F2 = P x A2 となります。
圧力は全体で同じであるため（F1/A1 = F2/A2）、出力力が出力ピストンと入力ピストンの面積比に比例することがわかります。出力ピストンの面積が入力ピストンの面積の10倍大きい場合、出力力は加えた力の10倍大きくなります。
トレードオフの理解
この力の倍増はどこからともなく現れるわけではありません。物理法則に従い、重要な妥協を伴います。
エネルギー保存の法則
エネルギーを何もないところから生み出すことはできません。出力力が倍増する一方で、出力ピストンが動く距離は比例して減少します。
大きなピストンを1インチ持ち上げるために、小さなピストンを10インチ押し下げる必要があるかもしれません。摩擦を無視すれば、（力 x 距離）である仕事量は、両側で同じままです。
「密閉された」システムの重要性
パスカルの原理は、完全に密閉されたシステムでのみ機能します。漏れがあると、圧力がかかったときに流体が逃げ出し、圧力が分散してシステム障害につながります。
流体の特性が重要
理想的で非圧縮性の流体を想定することが多いですが、実際の作動油には粘度（流れに対する抵抗）があり、気泡が含まれている場合があります。空気は非常に圧縮性が高いため、油圧ラインに存在するとシステムが「スポンジ状」に感じられ、効率が大幅に低下する可能性があります。
あなたのプロジェクトへの適用方法
この原理を理解することで、システムの設計とトラブルシューティングを効果的に行うことができます。あなたの特定の目標によって、法則のどの側面が最も重要かが決まります。
- 機械的優位性が主な焦点である場合：プレスやリフトジャッキで必要な力倍増を達成するために、出力ピストンと入力ピストンの面積比（A2/A1）を最大化することに集中します。
- システム効率が主な焦点である場合：漏れや内部圧縮によるエネルギー損失を最小限に抑えるために、完全に密閉されたシステムを作成し、高品質で非圧縮性の流体を使用することを優先します。
- 精密制御が主な焦点である場合：仕事のトレードオフを活用します。入力側での小さく管理しやすい動きは、出力側で非常に小さく強力で正確な動きに変換される可能性があり、これは車両のブレーキなどのシステムに最適です。
この原理を理解することで、単なる定義を知っている状態から、すべての油圧工学の背後にあるエレガントな力そのものを把握する状態へと移行します。
要約表：
| 側面 | 重要な洞察 |
|---|---|
| 定義 | 非圧縮性流体中の圧力変化は、均等かつ減衰なく伝達される。 |
| 力の倍増 | 出力力は面積比（F2 = F1 × (A2/A1)）に応じて増加する。 |
| トレードオフ | 力の増加は移動距離の減少と相殺される。エネルギーは保存される。 |
| 応用例 | 油圧ジャッキ、プレス、精密制御システムに使用される。 |
ラボの油圧ニーズにパスカルの法則を活用する準備はできましたか？ KINTEKは、自動ラボプレス、静水圧プレス、加熱ラボプレスなど、高性能ラボプレス機の専門メーカーです。当社の機器は、ラボでの用途において正確な力制御、耐久性、効率性を保証します。今すぐお問い合わせいただき、当社のソリューションがお客様のプロジェクトを最適化し、生産性を向上させる方法についてご相談ください！
ビジュアルガイド
関連製品
- 研究室のための熱された版が付いている自動高温によって熱くする油圧出版物機械
- 統合された熱い版が付いている手動熱くする油圧実験室の出版物 油圧出版物機械
- 真空ボックス実験室用ホットプレス向け加熱プレート付き加熱式油圧プレス機
- 研究室の油圧出版物 2T KBR FTIR のための実験室の餌出版物
- 研究室の油圧出版物の手袋箱のための実験室の餌の出版物機械
